duhocmy24h
duhocmy24h
Trang chủ Uncategorized Khảo sát sự biến thiên và lập bảng biến thiên của các hàm số sau: a) $y = - 2x + 3{\rm{ }}$trên $\mathbb{R}.$ b) $y = {x?

Khảo sát sự biến thiên và lập bảng biến thiên của các hàm số sau: a) $y = - 2x + 3{\rm{ }}$trên $\mathbb{R}.$ b) $y = {x?

Khảo sát sự trở thành thiên và lập bảng biến thiên của những hàm số sau: a) $y = - 2x + 3{\rm{ }}$trên $\mathbb{R}.$ b) $y = {x?

Khảo sát sự trở thành thiên và lập bảng biến thiên của những hàm số sau:

Bạn đang xem: Khảo sát sự biến thiên và lập bảng biến thiên của các hàm số sau: a) $y = - 2x + 3{\rm{ }}$trên $\mathbb{R}.$ b) $y = {x?

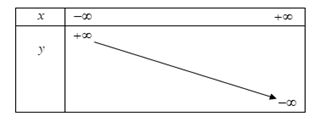
a) \(y = - 2x + 3{\rm{ }}\) bên trên \(\mathbb{R}.\)

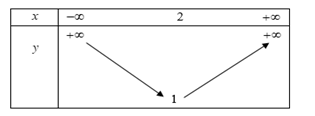
b) \(y = {x^2} - 4x + 5\) bên trên khoảng chừng \(\left( { - \infty ;2} \right)\) và bên trên khoảng chừng \(\left( {2; + \infty } \right).\)

Đáp án

a) Với từng \({{x}_{1}},{{x}_{2}}\in \mathbb{R}\) và \({x_1} < {x_2}\).
Ta với \(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \left( { - 2{x_1} + 3} \right) - \left( { - 2{x_2} + 3} \right) = - 2\left( {{x_1} - {x_2}} \right)\).
Suy rời khỏi \(\dfrac{{f\left( {{x_1}} \right) - f\left( {{x_2}} \right)}}{{{x_1} - {x_2}}} = \dfrac{{ - 2\left( {{x_1} - {x_2}} \right)}}{{{x_1} - {x_2}}} = - 2 < 0\).
Vậy hàm số nghịch ngợm trở thành bên trên \(\mathbb{R}\)Bảng trở thành thiên
84.PNG
b) Ta với \(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \left( {x_1^2 - 4{x_1} + 5} \right) - \left( {x_2^2 - 4{x_2} + 5} \right)\)\( = \left( {x_1^2 - x_2^2} \right) - 4\left( {{x_1} - {x_2}} \right) = \left( {{x_1} - {x_2}} \right)\left( {{x_1} + {x_2} - 4} \right)\). 

Xem thêm: KOH + Cl2 → KCl + KClO + H2O | KOH ra KCl | KOH ra KClO | Cl2 ra KCl | Cl2 ra KClO.

Với từng \({{x}_{1}},\,\,{{x}_{2}}\in \left( -\infty ;2 \right)\) và \({{x}_{1}}<{{x}_{2}}.\) Ta có
\(\left\{ \begin{align}
& {{x}_{1}}<2 \\
& {{x}_{2}}<2 \\
\end{align} \right.\Rightarrow {{x}_{1}}+{{x}_{2}}<4\) 

Do cơ \(\dfrac{{f\left( {{x_1}} \right) - f\left( {{x_2}} \right)}}{{{x_1} - {x_2}}} = \dfrac{{\left( {{x_1} - {x_2}} \right)\left( {{x_1} + {x_2} - 4} \right)}}{{{x_1} - {x_2}}} = {x_1} + {x_2} - 4 < 0\).
Vậy hàm số nghịch ngợm trở thành bên trên \(\left( {-\infty;2 } \right)\). 

Xem thêm: [TaiMienPhi.Vn] Công thức tính diện tích hình vuông, chu vi hình vuông kèm ví dụ

Với từng \({{x}_{1}},{{x}_{2}}\in \left( 2;+\infty \right)\) và \({{x}_{1}}<{{x}_{2}}.\) 

Ta có
\(\left\{ \begin{align}
& {{x}_{1}}>2 \\
& {{x}_{2}}>2 \\
\end{align} \right.\Rightarrow {{x}_{1}}+{{x}_{2}}>4\) 

Do cơ \(\dfrac{{f\left( {{x_1}} \right) - f\left( {{x_2}} \right)}}{{{x_1} - {x_2}}} = \dfrac{{\left( {{x_1} - {x_2}} \right)\left( {{x_1} + {x_2} - 4} \right)}}{{{x_1} - {x_2}}} = {x_1} + {x_2} - 4 > 0\).
Vậy hàm số đồng trở thành bên trên \(\left( {2; + \infty } \right)\).
Bảng trở thành thiên
85.PNG

BÀI VIẾT NỔI BẬT

Công thức tính bán kính mặt cầu oxyz trong toán học

Chủ đề Công thức tính bán kính mặt cầu oxyz Công thức tính bán kính mặt cầu Oxyz là công thức đơn giản và hữu ích giúp chúng ta tính toán kích thước của mặt cầu trong không gian ba chiều. Điều này giúp chúng ta dễ dàng xác định bán kính của mặt cầu, từ đó ứng dụng vào việc giải các bài toán liên quan đến hình học không gian. Công thức này đóng vai trò quan trọng trong việc xây dựng và phát triển kiến thức hình học.