TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI

MATHX.VN gửi cho tới quý cha mẹ và những em học viên tổng hợp Bộ 5 đề đánh giá thân thiện học tập kì II môn Toán lớp 8 (có đáp án kèm cặp điều giải chi tiết) sách mới mẻ. Cách diều - Kết nối học thức - Chân trời tạo nên. Học sinh rèn luyện lại kiến thức và kỹ năng tương đương thích nghi với những dạng toán vô đề ganh đua sau thời điểm ôn tập luyện qua loa đề cương bằng cơ hội trình diễn cụ thể điều giải đi ra vở. Chúc những con cái ôn tập luyện đảm bảo chất lượng và đạt thành phẩm cao vô kì ganh đua chuẩn bị tới!​

Phụ huynh và những em học viên coi thêm thắt đề ganh đua thân thiện kì 2 môn toán lớp 8 năm học tập 2023 - 2024 bên trên đây:

Bạn đang xem: TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI

TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 1

TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 2

TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 3

TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 4

TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 5

ĐỀ KIỂM TRA GIỮA HỌC KÌ II - TOÁN LỚP 8 - ĐỀ SỐ 5

NĂM HỌC: 2023 - 2024

Phần I. Trắc nghiệm

Phần II: Tự luận

Bài 1: Cho biểu thức: \(B={\dfrac{1}{x+1}}\,-\,{\dfrac{x^{3}-x}{x^{2}+1}}\,\cdot\,\left({\dfrac{1}{x^{2}+2x+1}}\,-\,{\dfrac{1}{x^{2}-1}}\right)\) (ĐKXĐ: x ≠ ± 1)

a) Rút gọn gàng B

b) Tính độ quý hiếm của B bên trên x = -2

c) Với độ quý hiếm năn nỉ của x thì B = 1

Lời giải: 

a) \(B={\dfrac{1}{x+1}}\,-\,{\dfrac{x^{3}-x}{x^{2}+1}}\,\cdot\,\left({\dfrac{1}{x^{2}+2x+1}}\,-\,{\dfrac{1}{x^{2}-1}}\right)\) (ĐKXĐ: x ≠ ± 1)

\(B=\dfrac{1}{x+1}-\dfrac{-2x}{(x^{2}+1)(x+1)}\)

\(B={\dfrac{x^{2}+1+2x}{(x^{2}+1)(x+1)}}\)

\(B={\dfrac{(x+1)^{2}}{(x^{2}+1)(x+1)}}\)

\(B={\dfrac{x+1}{x^{2}+1}}\)

Vậy \(B={\dfrac{x+1}{x^{2}+1}}\) với x ≠ ± 1

b) Thay x = -2 (TM) tao có: \(B=\dfrac{-2+1}{(-2)^{2}+1}=\dfrac{-1}{5}\)

c) \(B=1\Rightarrow{\dfrac{x+1}{x^{2}+1}}=1\Leftrightarrow x+1=x^{2}+1\Leftrightarrow x-x^{2}=0\)

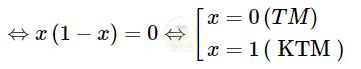
Vậy Lúc x = 0 thì B = 1

Bài 2: Giải những phương trình sau:

a) \(\dfrac{9x\!+\!5}{6}\;=1-\;\textstyle{\dfrac{6+3x}{8}}\)

b) \(\dfrac{x +1}{4}\;=\dfrac{1}{2}+\;\textstyle{\dfrac{2x+1}{5}}\)

c) \({\dfrac{2(x+1)}{3}}\,=\,{\dfrac{3}{2}}\,-\,{\dfrac{1{-}2x}{4}}.\)

Lời giải: 

a) \(\dfrac{9x\!+\!5}{6}\;=1-\;\textstyle{\dfrac{6+3x}{8}}\)

Xem thêm: KOH + Cl2 → KCl + KClO + H2O | KOH ra KCl | KOH ra KClO | Cl2 ra KCl | Cl2 ra KClO.

\({\dfrac{4(9x+5)}{24}}\,=\,{\dfrac{24}{24}}\,-\,{\dfrac{3(6+3x)}{24}}\)

\(36x+20=24-18-9x\)

36x + 9x = 6 - 20

45x = -14

\(x={\dfrac{-14}{45}}\)

Vậy \(x={\dfrac{-14}{45}}\)

b) \(\dfrac{x +1}{4}\;=\dfrac{1}{2}+\;\textstyle{\dfrac{2x+1}{5}}\)

\({\dfrac{5(x+1)}{20}}\,=\,{\dfrac{10}{20}}\,+\,{\dfrac{4(2x+1)}{5}}\)

5x + 5 = 10 + 8x + 4

5x - 8x = 14 - 5

-3x = 9

x = -3

Vậy x = -3

c) \({\dfrac{2(x+1)}{3}}\,=\,{\dfrac{3}{2}}\,-\,{\dfrac{1{-}2x}{4}}.\)

\(\dfrac{8(x+1)}{12}\,=\,\dfrac{18}{12}\,-\,\dfrac{3(1-2x)}{12}\)

8x + 8 = 18 - 3 + 6x

8x - 6x = 15 - 8

2x = 7

\(x={\dfrac{7}{2}}\)

Vậy \(x={\dfrac{7}{2}}\)

Bài 3: Tổng số học viên khối 8 và khối 9 của một ngôi trường là 580 em, vô cơ có 256 em là học viên xuất sắc. Tính số học viên của từng khối, hiểu được số học viên xuất sắc khối 8 lắc tỉ lệ 40% số học viên khối 8, số học viên xuất sắc khối 9 lắc tỉ trọng 48% số học viên khối 9.
 

Lời giải: 

Gọi số học viên khối 8 là x (học sinh). Điều kiện: x ∈ N*; x < 580.

Số học viên khối 9 là: 580 - x (học sinh)

Học sinh xuất sắc khối 8 là: 40%x = 0,4x (học sinh)

Số học viên xuất sắc khối 9 là: 48 (học sinh)

Vì cả nhì khối đem tổng cả 256 học viên xuất sắc nên tao đem phương trình:

\(0,4x+0,48\left(560-x\right)=256\)

\(0,4x+268,8-0,48x=256\)

\(0,4x-0,48x=256-268,8\)

-0,08x = -12,8

\(x=(-12,8):(-0,08)\)

x = 160 (tm)

Khi cơ, số học viên khối 9 là: 580 - 160 = 420 (học sinh)

Bài 4: Cho ΔABC đem những đàng cao BD và CE hạn chế nhau bên trên H. Chứng minh:

a) ΔHBE đồng dạng với ΔHCD.

b) \({\widehat{H D E}}={\widehat{H A E}}.\)

Lời giải: 

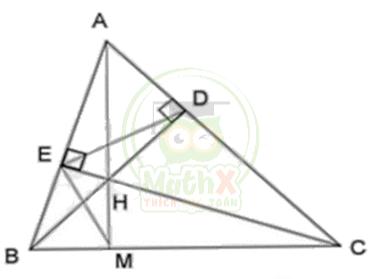
a) Xét ΔHBE và  ΔHCD có:

\(\widehat{B D C}=\widehat{C E B}=90^{0}\)

\({\widehat{E H B}}={\widehat{D E C}}\) (2 góc đối đỉnh)

=> ΔHBE~ ΔHCD (g - g) (điều nên hội chứng minh)

b) Theo câu a) tao có: ΔHBE~ ΔHCD => \({\dfrac{H E}{H D}}={\dfrac{H B}{H C}}\) hay \({\dfrac{H E}{H B}}={\dfrac{H D}{H C}}\)

Xét ΔHDE và ΔHBC tao có:

\({\dfrac{H E}{H B}}={\dfrac{H D}{H C}}\) (cmt)

\({\widehat{E H D}}={\widehat{BHC}}\) (2 góc đối đỉnh)

\({\widehat{HDE}}={\widehat{HAE}}\)

=> ΔHED ~ ΔHBC (c - g - c)

Mà đàng cao BD và CE cắt nhau tại H (theo fake thiết)

Suy đi ra H là trực tâm của ΔABC hoặc AH ⊥ BC bên trên M suy ra \({\widehat{A M B}}=90^{\circ}\)

Xét ΔAMB và ΔCEB có:

\({\widehat{C E B}}={\widehat{A M B}}=90^{0}\)

\({\widehat{B}}\) Chung

=> ΔAMB ~ ΔCEB (g - g)

=> \({\widehat{MAB }}={\widehat{ECB}}\) hay \({\widehat{HAE}}={\widehat{HCB}}\) 

Ta có: \({\widehat{HDE}}={\widehat{HAE}}\) (đpcm)

Bài 5: Cho \({\dfrac{a}{b+c}}\,+\,{\dfrac{b}{c+a}}\,+\,{\dfrac{c}{a+b}}\,=1\) . Chứng minh \({\dfrac{a^{2}}{b+c}}\,+\,{\dfrac{b^{2}}{c+a}}\,+\,{\dfrac{c^{2}}{a+b}}\,=\,0\)

Lời giải: 

Nhân cả hai vế của \({\dfrac{a}{b+c}}\,+\,{\dfrac{b}{c+a}}\,+\,{\dfrac{c}{a+b}}\,=1\) với a + b + c tao được

\({\dfrac{\mathrm{a}(a+b+\mathrm{c})}{{\mathrm{b}}+\mathrm{c}}}\,+\,{\dfrac{\mathrm{b}(a+{\mathrm{b}}+\mathrm{c})}{\mathrm{c}+{\mathrm{b}}}}\,+\,{\dfrac{\mathrm{c}(a+{\mathrm{b}}+\mathrm{c})}{{\mathrm{a}}+{\mathrm{b}}}}\,=\,\mathrm{a}\,+\,{\mathrm{b}}\,+\,\mathrm{c}\)

\({\dfrac{a^{2}+a(b+c)}{b+c}}\,+\,{\dfrac{b^{2}+b(c+a)}{c+a}}\,+\,{\dfrac{c^{2}+c(a+b)}{a+b}}\,=\,a\,+\,b+c\)

\({\dfrac{a^{2}}{b+c}}+a+{\dfrac{b^{2}}{c+a}}+b+{\dfrac{c^{2}}{a+b}}+c=a+b+c\)

Xem thêm: Tập tính kiếm ăn của động vật

\({\dfrac{\mathbf{a}^{2}}{\mathbf{b}+\mathbf{c}}}\,+\,{\dfrac{\mathbf{b}^{2}}{\mathbf{c}+\mathbf{a}}}\,+\,{\dfrac{\mathbf{c}^{2}}{\mathbf{a}+\mathbf{b}}}\,=\,0\) (đpcm)

Trên đây MATHX đang được chỉ dẫn những em giải đề ganh đua thân thiện kì 2 môn toán lớp 8 năm học tập 2023 - 2024 - đề 5. Ngoài ra các bậc phụ huynh cần mang lại con em mình mình học chính cách thức và tìm hiểu thêm những khóa học tập online tại MATHX.VN để chung con cái thoải mái tự tin đoạt được môn toán nhé.