Công thức tính diện tích tam giác thường, vuông, cân, vuông cân, đều

Trong quy trình học tập toán, những Việc đem sự xuất hiện tại của hình tam giác vô cùng phổ cập. Việc chuẩn bị cho bản thân mình những kiến thức và kỹ năng về hình tam giác và công thức tính diện tích S tam giác là vô nằm trong quan trọng. Dưới phía trên, Truonghoc247 share về những loại tam giác thông thường gặp gỡ và công thức tính diện tích S của chúng!

Tam giác là gì?

Tam giác (hình tam giác) là 1 nhập số những mô hình học tập cơ bạn dạng và phổ cập. Hình tam giác đem Điểm lưu ý là hình phẳng lặng nhập không khí 2 chiều, được kết cấu vì thế 3 điểm nối ko trực tiếp mặt hàng, 3 điểm là 3 đỉnh của tam giác, những đoạn trực tiếp nối 3 đặc điểm này là cạnh của tam giác. Tam giác là nhiều giác đem không nhiều cạnh nhất (3 cạnh), tổng 3 góc nhập tam giác là 180 chừng.

Bạn đang xem: Công thức tính diện tích tam giác thường, vuông, cân, vuông cân, đều

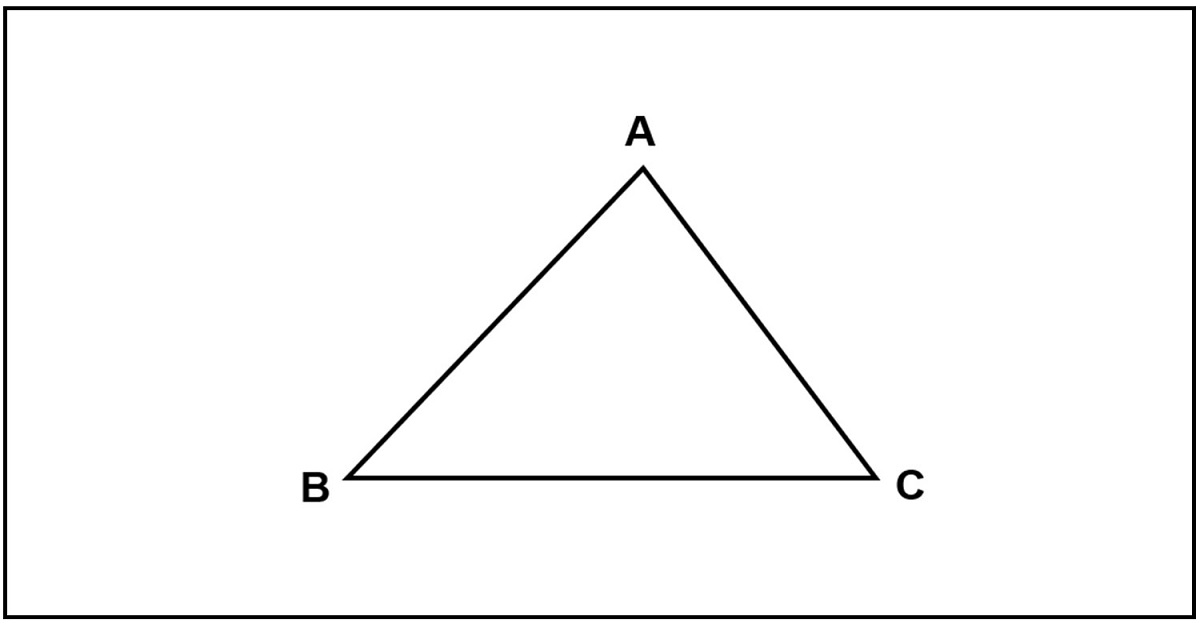
Ví dụ: Hình tam giác ABC bao gồm 3 cạnh (cạnh AB, BC, AC), 3 đỉnh (đỉnh A, B, C), 3 góc nhập (góc ABC, BCA, CAB). Dường như tam giác còn tồn tại 6 góc ngoài được tạo ra vì thế góc kề bù và góc nhập của tam giác.

Các loại tam giác thông thường gặp

Trong hình học tập, phụ thuộc vào những điểm riêng rẽ của cạnh tam giác, góc tam giác tuy nhiên hình tam giác được chia nhỏ ra thực hiện nhiều loại như tam giác vuông, tam giác cân nặng, tam giác đều,… Trong toán học tập, việc xác lập những loại tam giác cũng vào vai trò vô cùng cần thiết nhằm tính đúng đắn những độ dài rộng như diện tích S, chu vi hoặc phụ thuộc vào Điểm lưu ý của từng loại tam giác nhằm suy đoán đặc thù, cơ hội giải của Việc. Dưới đấy là những loại tam giác thông thường gặp:

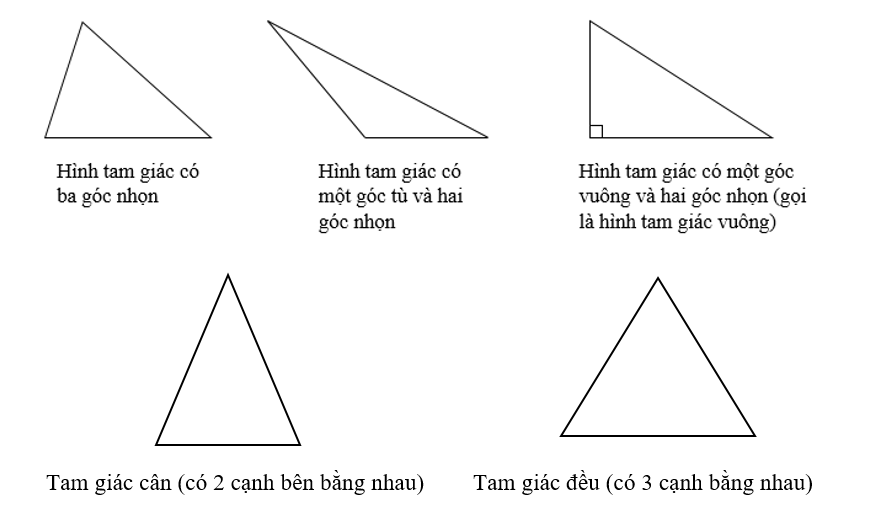
Tam giác thường

Tam giác thông thường là hình dáng tam giác cơ bạn dạng nhất. Loại tam giác thông thường không tồn tại gì đặc trưng, những cạnh đem chiều nhiều năm không giống nhau, số đo những góc không giống nhau.

Tam giác tù

Tam giác tù là tam giác mang 1 góc là góc tù (góc to hơn 90 độ) và 2 góc còn sót lại là góc nhọn. Trong những dạng bài bác tập dượt thông thường không nhiều nói đến dạng tam giác này vì thế nó không tồn tại Điểm lưu ý gì quá khác lạ đối với tam giác thông thường và thỉnh thoảng còn được xem là một tam giác thông thường.

Tam giác nhọn

Tam giác nhọn là loại tam giác đem 3 góc nhập đều là góc nhọn (góc nhỏ rộng lớn 90 độ). Tương tự động như tam giác tù, tam giác nhọn cũng không tồn tại Điểm lưu ý, đặc thù gì đặc trưng và thông thường được đánh giá như tam giác thông thường trong những dạng bài bác tập dượt toán.

Tam giác vuông

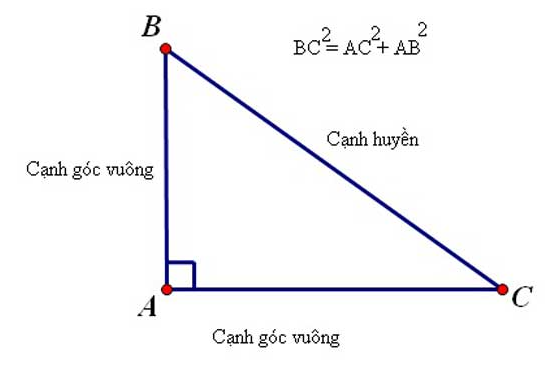
Tam giác vuông là hình tam giác có một góc là góc vuông (góc vì thế 90 độ). Trong tam giác vuông, cạnh đối lập góc vuông được gọi là cạnh huyền là cạnh đem chiều nhiều năm lớn số 1 nhập tam giác, 2 cạnh tạo ra trở nên góc vuông gọi là cạnh góc vuông. Vì vẫn có một góc vuông vì thế 90 chừng nên tổng 2 góc còn sót lại vì thế 90 chừng.

Tam giác vuông xuất hiện tại thật nhiều trong những dạng bài bác tập dượt toán kể từ những lớp tè học tập đi học 12. Định lý toán học tập nối sát với tam giác vuông là ấn định lý pytago: “Bình phương cạnh huyền vì thế tổng bình phương nhì cạnh góc vuông”.

Ví dụ: Tam giác ABC vuông bên trên A đem góc BAC = 90 chừng. Theo ấn định lý pytago: BC^2 = AB^2 + AC^2

Tam giác cân

Tam giác cân nặng là hình tam giác đem chiều nhiều năm nhì cạnh không giống nhau gọi là nhì cạnh mặt mày, đem 2 góc lòng cân nhau. 2 cạnh mặt mày dẫn đến 1 góc gọi rời khỏi góc ở đỉnh, 2 góc còn sót lại là 2 góc lòng. Với đặc thù đặc trưng cả về cạnh và góc nhập tam giác, tam giác cân nặng xuất hiện tại phổ cập nhập nhiều dạng khác nhau Việc học tập.

Ngoài rời khỏi, tam giác cân nặng đàng cao kẻ kể từ đỉnh bên cạnh đó là đàng trung tuyến của tam giác cân nặng tiếp tục trải qua trung điểm của cạnh lòng.

Ví dụ: Tam giác ABC, cân nặng bên trên A đem AB = AC, góc ABC = góc Ngân Hàng Á Châu ACB, AH là đàng cao và là đàng trung tuyến của tam giác

Tam giác vuông cân

Như tên thường gọi, tam giác vuông cân nặng là tam giác quy tụ Điểm lưu ý của tất cả tam giác vuông và tam giác cân nặng. Tam giác vuông cân nặng có một góc vuông (góc 90 độ), 2 cạnh góc vuông cân nhau, 2 góc lòng là 2 góc nhọn cân nhau và đều vì thế 45 chừng. Trong tam giác vuông cân nặng, đàng cao, đàng trung tuyến, đàng phân giác kẻ kể từ đỉnh góc vuông trùng nhau và vì thế ½ cạnh huyền.

Ví dụ: Tam giác vuông cân nặng ABC, vuông cân nặng bên trên A đem góc BAC vì thế 90 chừng, góc ABC = góc Ngân Hàng Á Châu ACB = 45 chừng, cạnh AB = AC, cạnh BC là cạnh huyền và bám theo ấn định lý pytago thì BC^2= AB^2 + AC^2. Đường cao AH là đàng phân giác, đàng trung tuyến của tam giác ABC và AH = ½ BC.

Tam giác đều

Tam giác đều là 1 dạng tam giác đặc trưng của tam giác cân nặng. Nếu tam giác cân nặng chỉ mất 2 cạnh mặt mày cân nhau và 2 góc lòng cân nhau thì tam giác đều sở hữu cả 3 cạnh tam giác cân nhau và 3 góc đều cân nhau (bằng 60 độ).

Ví dụ: Tam giác đều ABC đem AB = BC = AC, góc ABC = góc BCA = góc BAC = 60 độ

Đường cao và lòng tam giác

Đường cao của tam giác là đoạn trực tiếp kẻ từ là 1 đỉnh và vuông góc với cạnh đối lập của đỉnh tê liệt. Mỗi tam giác chỉ mất thân phụ đàng cao. Ba đàng cao của một tam giác đồng quy bên trên một điểm thì đặc điểm này được gọi là trực tâm của hình tam giác.

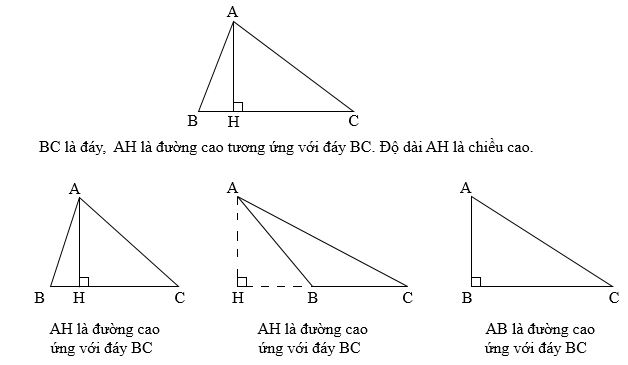
Một cạnh nhập tam giác được gọi là cạnh lòng Lúc cạnh tê liệt vuông góc với đàng cao nhập tam giác.

Diện tích tam giác thông thường được xem bám theo công thức: (chiều cao x cạnh đáy)/2

Ví dụ: Diện tích tam giác ABC đem chiều nhiều năm lòng là 3m và độ cao là 2,1m. Diện tích tam giác ABC là: S= (3 * 2.1)/2 = 3.15 m2

Tuỳ bám theo từng cấp cho học tập và bám theo đề bài bác tuy nhiên sẽ sở hữu phương pháp tính diện tích S tam giác theo khá nhiều công thức không giống nhau như: tính diện tích S lúc biết 1 góc và chiều nhiều năm 2 cạnh kề hoặc tính diện tích S tam giác lúc biết chừng nhiều năm 3 cạnh bám theo công thức Heron, tính diện tích S vì thế nửa đường kính đàng tròn trĩnh nước ngoài tiếp tam giác, tính diện tích S vì thế nửa đường kính đàng tròn trĩnh nội tiếp tam giác,…

Công thức tính diện tích S tam giác vuông

Công thức tính diện tích S tam giác vuông là: S= ½ ab, nhập tê liệt a, b đó là chừng nhiều năm ứng của 2 cạnh góc vuông.

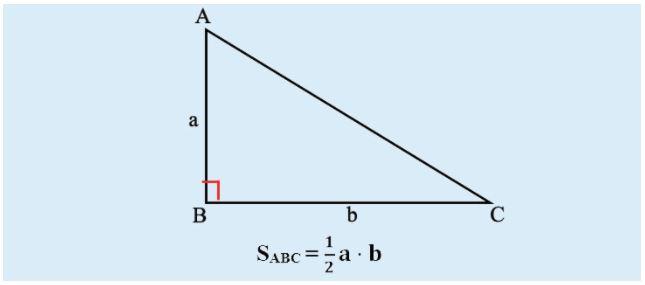
Ví dụ: Tam giác ABC vuông bên trên A đem AB=3cm, AC= 4cm thì S= ½ * 3 * 4=6cm

Công thức tính diện tích S tam giác cân

Tam giác cân nặng đem công thức tính tương tự động như tam giác thường: S = ½ *(a * h)

Trong đó: h là đàng cao kẻ từ là một đỉnh của tam giác đều và a là chiều nhiều năm của cạnh đối mà đàng cao h trải qua.

Xem thêm: Bảng đầy đủ các công thức đạo hàm và đạo hàm lượng giác

Công thức tính diện tích S tam giác vuông cân

Tam giác vuông cân nặng đem 2 cạnh góc vuông tiếp tục cân nhau và diện tích tam giác vuông cân sẽ tiến hành tính vì thế ½ a2, nhập tê liệt a đó là chừng nhiều năm của cạnh góc vuông cân nặng.

Công thức tính diện tích S tam giác đều

Ngoài công thức tính diện tích S tam giác như tam giác thông thường, công thức tính diện tích S tam giác đều phổ cập trong tương đối nhiều Việc này đó là ấn định lý Heron:

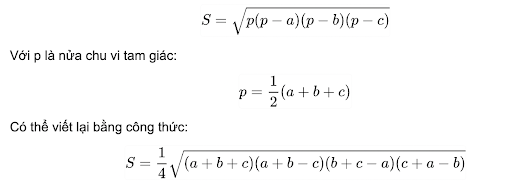
Công thức tính diện tích S tam giác nhập hệ toạ chừng Oxyz

Khi học tập toán hình, ngoài ra dạng toán giản dị nhập không khí 2 chiều thì sẽ sở hữu những dạng toán nhập không khí 3 chiều. Khi tê liệt, tớ cần thiết phần mềm công thức hệ trục toạ chừng Oxyz nhằm tính diện tích S tam giác: SABC= ½ [AB;AC]

Trong tê liệt [AB;AC] được xem như sau:

Gọi tọa chừng điểm A là A (a1, b1, c1); tọa chừng điểm B là B (a2, b2, c2); tọa chừng điểm C là C (a3, b3, c2). Theo tê liệt, AB = (a2-a1; b2-b1; c2-c1); AC = (a3-a1; b3-b1; c3-c1). Từ tê liệt tớ đem cơ hội tính: [AB;AC]= ( b2−b1 c2−c1) b3−b1 c3−c1 ; c2−c1 a2−a1 c3−c1 a3−a1; ; a2−a1 b2−b1 a3−a1 b3−b1 )

Sau tê liệt tất cả chúng ta trừ chéo cánh từng biểu thức lẫn nhau sẽ sở hữu được sản phẩm của [AB;AC] là tọa chừng bao gồm 3 điểm.

Một số dạng bài bác thói quen diện tích S tam giác

Dưới đấy là một số trong những dạng bài bác thói quen diện tích S tam giác phổ biến:

Dạng 1: thạo độ cao và chừng nhiều năm lòng tính diện tích S tam giác

Ví dụ 1: Tính diện tích S tam giác thông thường ABC đem chiều nhiều năm lòng BC=20cm và độ cao AH=13cm

Bài làm: Diện tích tam giác ABC = (20*13)/2= 130cm2

Ví dụ 2: Tính diện tích S tam giác vuông DEF vuông bên trên E đem 2 cạnh góc vuông ED= 4dm, EF=5dm

Bài làm: Diện tích tam giác DEF = ½*4*5=10dm2

Dạng 2: Tính chừng nhiều năm cạnh lòng lúc biết diện tích S và độ cao của tam giác

Từ công thức tính diện tích S tam giác S=(a*h)/2, suy ra sức thức tính chừng nhiều năm cạnh lòng a=(S*2)/h

Ví dụ: Tính chừng nhiều năm cạnh lòng BC của hình tam giác thông thường ABC đem độ cao AH vì thế 10cm và diện tích S là 100cm2.

Bài làm: Độ nhiều năm BC=(100*2)/10=20cm

Dạng 3: Tính độ cao lúc biết diện tích S và chừng nhiều năm đáy

Từ công thức tính diện tích S tam giác S=(a*h)/2, suy ra sức thức tính độ cao h=(S*2)/a

Ví dụ: Tính độ cao AH của hình tam giác ABC có tính nhiều năm cạnh lòng BC= 7cm và diện tích S vì thế 168cm2.

Bài làm: Chiều cao AH=(168*2)/7=12cm

Mẫu bài bác tập dượt tự động luyện diện tích S tam giác

Dưới đấy là một số trong những bài bác tập dượt về tính chất diện tích S tam giác:

Bài 1:

Tính diện tích S tam giác có:

Độ nhiều năm lòng là 13cm và độ cao là 8cm
Độ nhiều năm lòng là 5.6dm và độ cao là 1 trong.2dm

Đáp án:

52cm2
3.36cm2

Bài 2:

Tính diện tích S tam giác vuông có tính nhiều năm 2 cạnh góc vuông theo thứ tự là:

72cm và 24cm
11.4 centimet và 22.9cm

Đáp án:

Xem thêm: Định nghĩa đường trung tuyến là gì? Công thức tính đường trung tuyến

864cm2
130.53cm2

Bài 3:

Cho hình tam giác BCD, biết chừng nhiều năm lòng là 5m và độ cao là 4m. Tính diện tích S của tam giác BCD?

Đáp án: S=10m2

Trên đấy là những công thức tính diện tích S tam giác phổ cập. Hy vọng những kiến thức và kỹ năng tuy nhiên Truonghoc247 tổ hợp nhập nội dung bài viết này tiếp tục hữu ích với các bạn.