Định nghĩa đường trung tuyến là gì? Công thức tính đường trung tuyến

Số lượt gọi bài bác viết: 150.693

Định nghĩa lối trung tuyến là gì? Tính hóa học của lối trung tuyến? Công thức tính phỏng lâu năm lối trung tuyến? Đặc điểm của lối trung tuyến? Lý thuyết và những dạng bài bác tập luyện về khái niệm lối trung tuyến?… Hãy nằm trong DINHNGHIA.VN lần hiểu cụ thể về chủ thể lối trung tuyến cũng tựa như những nội dung tương quan qua quýt nội dung bài viết rõ ràng tiếp sau đây nhé!. 

Bạn đang xem: Định nghĩa đường trung tuyến là gì? Công thức tính đường trung tuyến

Định nghĩa lối trung tuyến là gì? 

Đường trung tuyến của một đoạn thẳng là 1 trong những đường thẳng liền mạch trải qua trung điểm của đoạn trực tiếp cơ.

Định nghĩa lối trung tuyến của tam giác

Trong hình học tập thì lối trung tuyến của một tam giác được khái niệm là 1 trong những đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập. Mỗi tam giác sẽ sở hữu được 3 lối trung tuyến.

Ví dụ:

Theo như hình vẽ bên trên thì những đoạn trực tiếp AI, công nhân, BM được xem là 3 trung tuyến của tam giác ABC.

Tính hóa học của lối trung tuyến nhập tam giác

• Ba lối trung tuyến của tam giác nằm trong trải qua một điểm. Điểm cơ cơ hội đỉnh một khoảng tầm bởi \(\frac{2}{3}\) phỏng lâu năm lối trung tuyến trải qua đỉnh ấy.
• Giao điểm của tía lối trung tuyến gọi là trọng tâm.
• Vị trí của trọng tâm tam giác: Trọng tâm của một tam giác cơ hội từng đỉnh một khoảng tầm bởi 2/3 phỏng lâu năm lối trung tuyến trải qua đỉnh ấy.

Ví dụ:  

Gọi G là trọng tâm của tam giác ABC, ABC sở hữu những trung tuyến AI, BM, công nhân thì tao sẽ sở hữu được biểu thức:

\(\frac{AG}{AI}\) = \(\frac{BG}{BM}\) = \(\frac{CG}{CN}\) = \(\frac{2}{3}\)

Một số tấp tểnh lý lối trung tuyến nhập tam giác

Thực hành: Cắt một tam giác bởi giấy tờ. Gấp lại nhằm xác lập trung điểm một cạnh của chính nó. Kẻ đoạn trực tiếp nối trung đặc điểm này với đỉnh đối lập. bằng phẳng cơ hội tương tự động, hãy vẽ tiếp hai tuyến đường trung tuyến sót lại.

Quan sát tam giác một vừa hai phải hạn chế (trên này đã vẽ tía lối trung tuyến). Cho biết: Ba lối trung tuyến của tam giác này còn có nằm trong trải qua một điểm mạnh không?

 Định lý 1: Ba lối trung tuyến của một tam giác nằm trong trải qua một điểm. điểm gặp gỡ nhau của 3 lối trung tuyến gọi là trọng tâm (centroid) của tam giác cơ.

Định lý 2: Đường trung tuyến của tam giác phân chia tam giác ấy trở nên nhì tam giác sở hữu diện tích S đều nhau. Ba trung tuyến phân chia tam giác trở nên 6 tam giác nhỏ với diện tích S đều nhau.

Ví dụ minh họa:

Tam giác \(\Delta ABC\) sở hữu D, E, F là BC, CA, AB. Khi cơ AD, BE, CF theo thứ tự là những lối trung tuyến khởi nguồn từ tía đỉnh A, B, C. AD, BE, CF đồng quy ở G.

Ta sở hữu G là trọng tâm của tam giác \(\Delta ABC\).

Theo khái niệm, AE=EC, CD=DB, BF= FA, bởi đó:

\(S\Delta AGE=S\Delta CGE;S\Delta BGD=S\Delta CGD; S\Delta AGF=S\Delta BGF \) nhập cơ kí hiệu \(S\Delta ABC \) là diện tích S của tam giác ABC.

Điều này chính bởi trong những tình huống nhì tam giác sở hữu chiều lâu năm lòng đều nhau, và sở hữu nằm trong lối cao kể từ lòng, nhưng mà diện tích S của một tam giác thì bởi 50% chiều lâu năm lòng nhân với lối cao, lúc đó nhì tam giác ấy sở hữu diện tích S đều nhau.

Chúng tao có: 

\(S\Delta ACG=S\Delta ACD-S\Delta CGD;S\Delta ABG=S\Delta ABD-S\Delta BGD \)

Do cơ tao sở hữu :\(S\Delta ABG=S\Delta ACG\) và \(S\Delta DBG=S\Delta DCG\); \(S\Delta CDG=\frac{1}{2}S\Delta ACG\)

Do \(S\Delta BGF=S\Delta AGF\), \(S\Delta AGF=\frac{1}{2}S\Delta ACG=S\Delta BGF=\frac{1}{2}S\Delta BCG\)

Do vậy, \(S\Delta AFG=S\Delta BFG=S\Delta BGD=S\Delta CGD\)

Sử dụng nằm trong cách thức này. tao hoàn toàn có thể chứng tỏ điều sau:

\(S\Delta AFG=S\Delta BFG=S\Delta BGD=S\Delta CGD=S\Delta CGE= S\Delta AGE \)

Định lý 3 : Về địa điểm trọng tâm: Trọng tâm của một tam giác cơ hội từng đỉnh một khoảng tầm bởi \(\frac{2}{3}\) phỏng lâu năm lối trung tuyến qua quýt đỉnh ấy.

Ví dụ như sau:

Tam giác \(\Delta ABC\) sở hữu AD, BE, CF theo thứ tự là những lối trung tuyến khởi nguồn từ tía đỉnh A, B, C. Theo tấp tểnh lý 1 thì tía lối này đồng quy bên trên một điểm gọi là vấn đề G. 

Theo tấp tểnh lý 2 thì:

\(AG=\frac{2}{3}AD; BG=\frac{2}{3}BE; CG=\frac{2}{3}CF\)

Định nghĩa lối trung tuyến nhập tam giác đặc biệt

Tìm hiểu lối trung tuyến nhập tam giác vuông

Tam giác vuông là một tình huống quan trọng đặc biệt của tam giác, nhập cơ, tam giác sẽ sở hữu được một góc có tính rộng lớn là 90 phỏng, và nhì cạnh tạo ra góc này vuông góc cùng nhau.

Chính vì vậy nhưng mà lối trung tuyến của tam giác vuông sẽ sở hữu được tương đối đầy đủ những đặc thù của một lối trung tuyến tam giác.

Trong một tam giác vuông, lối trung tuyến ứng với cạnh huyền bởi nửa cạnh huyền.

Một tam giác sở hữu trung tuyến ứng với 1 cạnh bởi nửa cạnh cơ thì tam giác ấy là tam giác vuông.

Ví dụ 1:

Tam giác ABC vuông ở B, phỏng lâu năm lối trung tuyến BM tiếp tục bởi MA, MC và bởi \(\frac{1}{2}\) AC

Ngược lại nếu như BM = \(\frac{1}{2}\) AC thì tam giác ABC tiếp tục vuông ở B.

Ví dụ 2: 

Tam giác \(\Delta ABC\) vuông ở A, phỏng lâu năm lối trung tuyến AM tiếp tục bởi MB, MC và bởi \(\frac{1}{2}\)  BC.

Ngược lại nếu như AM = \(\frac{1}{2}\) BC thì tam giác \(\Delta ABC\) tiếp tục vuông ở A.

Chứng minh:

Cho tam giác \(\Delta ABC\). Gọi M là trung điểm của BC. Chứng minh rằng:

1. Nếu = 900 thì MA = \(\frac{1}{2}\) BC
2. Nếu MA = \(\frac{1}{2}\) BC thì góc \(\widehat{A}\) = 900.

Xét tam giác \(\Delta ABC\) sở hữu M là trung điểm của BC.

Trên tia đối của tia MA lấy điểm N sao mang lại MN = MA.

Ta có:

\(\widehat{AMB}\) = \(\widehat{NMC}\) (đối đỉnh)

BM = CM (giả thiết)

MA = MN (dựng hình)

Suy ra: tam giác  tam giác \(\Delta MAB\) = tam giác  tam giác \(\Delta MNC\) (c.g.c)

Suy ra: NC = AB và \(\widehat{MBA}\) = \(\widehat{MCN}\)

1800. a) Do  \(\widehat{MBA}\) = \(\widehat{MCN}\) nên AB // NC suy đi ra \(\widehat{BAC}\) +  \(\widehat{ACN}\) = 1800.

Nếu góc \(\widehat{BAC}\)  = 900 thì góc \(\widehat{ACN}\) = 900.

Khi cơ tao có: tam giác \(\Delta ABC\) =  tam giác \(\Delta CNA\) (c.g.c) vì thế sở hữu AC chung; AB = NC (cmt) và  \(\widehat{BAC}\)= \(\widehat{ACN}\) = 900.

Ta có: AN = BC => AM =  \(\frac{1}{2}\) BC

1. b) Ta có: MA = \(\widehat{A}\) AN. Nếu MA =\(\widehat{A}\) BC thì AN = BC.

Lại sở hữu AB = công nhân (cmt)

Xem thêm: Cơ sở tế bào học của việc tạo giống thuần dựa trên nguồn biến dị tổ hợp là

Suy đi ra tam giác \(\Delta ABC\) =  tam giác \(\Delta CNA\) (c.c.c), suy ra: góc \(\widehat{BAC}\) = góc \(\widehat{ACN}\)

Mà \(\widehat{BAC}\) + \(\widehat{ACN}\)  = 1800 (vì AB // CA) nên  \(\widehat{BAC}\) = 900 (dpcm)

Bài tập luyện ví dụ: Cho tam giác vuông ABC sở hữu nhì cạnh góc vuông AB = 3cm, AC = 4cm. Tính khoảng cách kể từ đỉnh A cho tới trọng tâm G của tam giác ABC.

Gợi ý giải: Sử dụng đặc thù lối trung tuyến của tam giác vuông: lối trung tuyến ứng với cạnh huyền thì có tính lâu năm bởi 50% cạnh huyền và tấp tểnh lý Pitago. 

Tìm hiểu lối trung tuyến nhập tam giác cân nặng, tam giác đều

Tính chất: Đường trung tuyến nhập tam giác cân nặng (và tam giác đều)  ứng với cạnh lòng thì vuông góc với kiểu mẫu đấy và phân chia tam giác những trở nên nhì tam giác đều nhau.

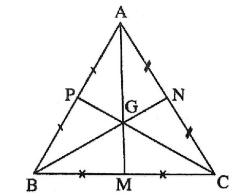
Tam giác đều \(\Delta ABC\) sở hữu AM, BN, CP theo thứ tự là tía lối trung tuyến của tam giác. Theo đặc thù của lối trung tuyến nhập tam giác đều tao có:

\(AM\bot BC; BN\bot AC; CP\bot AB\)

và \(\Delta ABM=\Delta ACM; \Delta ABN=\Delta CBN; \Delta ACP=\Delta BCP \).

Bài tập luyện ví dụ:

Chứng minh nhập một tam giác cân nặng thì hai tuyến đường trung tuyến ứng với nhì cạnh mặt mày thì bởi nhau

Chứng minh tấp tểnh lý hòn đảo của tấp tểnh lý trên: Nếu tam giác sở hữu 2 lối trung tuyến đều nhau thì tam giác cơ cân nặng.

Công thức tương quan cho tới phỏng lâu năm của trung tuyến

 Ta hoàn toàn có thể tính được phỏng lâu năm lối trung tuyến của một tam giác trải qua phỏng lâu năm những cạnh của tam giác ấy. Độ lâu năm của trung tuyến được xem bởi tấp tểnh lý Apollonius như sau:

Trong cơ a, b và c là những cạnh của tam giác với những trung tuyến ứng \(m_{a}, m_{b}, m_{c}\) kể từ trung điểm.

Vậy là tao tiếp tục lần hiểu khá tương đối đầy đủ về khái niệm và đặc thù của lối trung tuyến, giống như vận dụng nó nhập một trong những tình huống quan trọng đặc biệt. Sau trên đây tất cả chúng ta hãy rèn luyện trải qua một trong những bài bác tập luyện giản dị và đơn giản nhé.

Một số bài bác tập luyện lối trung tuyến lớp 7

Ví dụ 1: Cho hai tuyến đường trực tiếp x’x và y’y  gặp gỡ nhau ở O. Trên tia Ox lấy nhì điểm A và B sao mang lại A nằm trong lòng O và B, AB=2OA. Trên y’y  lấy nhì điểm L và M sao mang lại O là trung điểm của đoạn trực tiếp LM. Nối B với L, B với M và gọi P.. là trung điểm của đoạn trực tiếp MB, Q là trung điểm của đoạn trực tiếp LB.  Chứng minh những đoạn trực tiếp LP và MQ trải qua A.

Cách giải:

Ta sở hữu O là trung điểm của đoạn LM (gt)

 Suy đi ra BO là lối trung tuyến của \(\Delta BLM\) (1)

Mặt không giống BO = BA + AO vì thế A nằm trong lòng O, B hoặc BO = 2 AO + AO= 3AO vì thế AB = 2AO (gt)

Suy đi ra \(AO= \frac{1}{3} BO\) hoặc \(BA= \frac{2}{3} BO\) (2)

Từ (1) và (2) suy đi ra A là trọng tâm của \(\Delta BLM\) ( đặc thù của trọng tâm)

 mà LP và MQ  là những lối trung tuyến của \(\Delta BLM\) vì thế P.. là trung điểm của đoạn trực tiếp MB (gt)

 suy đi ra những đoạn trực tiếp LP và MQ đều trải qua A ( đặc thù của tía lối trung tuyến) 

 Ví dụ 2: Cho \(\Delta ABC\) sở hữu BM, công nhân là hai tuyến đường trung tuyến hạn chế nhau bên trên G. Kéo lâu năm BM lấy đoạn ME=MG. Kéo lâu năm công nhân lấy đoạn NF=NG. Chứng minh:

1. EF=BC
2. Đường trực tiếp AG trải qua trung điểm BC.

Cách giải:

a.) Ta sở hữu BM và công nhân là hai tuyến đường trung tuyến gặp gỡ nhau bên trên G nên G là trọng tâm của tam giác \(\Delta ABC\). 

\(\Rightarrow GC=2GN\)

mà \(FG=2GN \Rightarrow GC=GF\)

Tương tự động BG, GE và \(\widehat{G_{1}}=\widehat{G_{2}}\) (đd). Do cơ \(\Delta BGC=\Delta EGF (c.g.c))\)

Suy đi ra BC=EF

b.) G là trọng tâm nên AG đó là lối trung tuyến loại tía nhập tam giác ABC

 nên AG trải qua trung điểm của BC. 

Trắc nghiệm đặc thù tía lối trung tuyến của tam giác

Câu 1: Chọn câu sai:

1. Trong một tam giác sở hữu 3 lối trung tuyến
2. Các lối trung tuyến của tam giác hạn chế nhau bên trên một điểm
3. Giao của tía lối trung tuyến của một tam giác gọi là trọng tâm của tam giác đó
4. Một tam giác sở hữu nhì trọng tâm

Câu 2:  Điền số phù hợp nhập địa điểm chấm:”Trọng tâm của một tam giác cơ hội từng đỉnh một khoảng tầm bằng… phỏng lâu năm lối trung tuyến trải qua đỉnh ấy”

1. \(\frac{2}{3}\)
2. \(\frac{3}{2}\)
3. 2
4. 3

Câu 3: Cho tam giác \(\Delta ABC\) sở hữu lối trung tuyến AM = 9cm và trọng tâm G. Độ lâu năm đoạn AG là:

1. 4.5 cm
2. 3 cm
3. 6 cm
4. 4 cm

Bài tập luyện thực hành thực tế lối trung tuyến nhập tam giác

Bài 1: Cho tam giác \(\Delta ABC\) , với AM là lối trung tuyến , biết lối trung tuyến \(AM=\frac{1}{2}BC\), hãy chứng tỏ rằng tam giác \(\Delta ABC\)vuông ở góc cạnh A:

Bài 2: Cho tam giác vuông \(\Delta ABC\) với góc A là góc vuông, sở hữu cạnh AB = 18cm, cạnh  AC = 24cm, hãy tính tổng những khoảng cách kể từ trọng tâm G của tam giác cho tới những đỉnh của tam giác \(\Delta ABC\).

Bài 3: Cho tam giác \(\Delta ABC\), lối trung tuyến của tam giác là đoạn BM, bên trên đoạn trực tiếp BM lấy nhì điểm G và K sao mang lại đoạn trực tiếp BG = BM và G là trung điểm của BK, gọi điểm N là trung điểm của KC , GN hạn chế CM ở điểm O, hãy chứng tỏ :

• \(GO=\frac{1}{3}BC\)
• O là trọng tâm của tam giác GKC

Bài 4: Cho tam giác \(\Delta ABC\), bên trên cạnh đối của cạnh AB , hãy lấy điểm D sao mang lại đoạn trực tiếp AD = AB, bên trên cạnh AC lấy điểm E sao mang lại đoạn trực tiếp AE = 1/3 AC, đoạn trực tiếp BE hạn chế CD ở điểm M, chúng ta hãy chứng tỏ \(AM=\frac{1}{2}BC\)  và M là trung điểm của CD.

Bài 5: Cho điểm G là trọng tâm của tam giác đều \(\Delta ABC\), chúng ta hãy chứng minh rằng những cạnh GA , GB , GC đều nhau.

Bài 6: Cho 1 tam giác \(\Delta ABC\) cân nặng ở A có AB = AC = 17cm, BC= 16cm, hãy kẻ lối trung tuyến AM. Tính độ dài AM và chứng minh: AM vuông góc với BC.

Bài 7:Gọi G là trọng tâm của tam giác \(\Delta ABC\). Trên tia AG lấy điểm G’ sao mang lại G là trung điểm của AG’. So sánh những cạnh của tam giác BGG’ với những lối trung tuyến của tam giác \(\Delta ABC\). So sánh những lối trung tuyến của tam giác BGG’ với những cạnh của tam giác \(\Delta ABC\).

Bài 8: Cho tam giác ABC sở hữu góc A bởi 90 phỏng. D là trung điểm của BC. Trên tia đối của tia DA lấy điểm E sao mang lại DE=DA. Chứng minh tam giác ABD = tam giác ECD. Tính AD biết AB=6cm, AC= 8cm.

Các dạng toán thông thường gặp gỡ về lối trung tuyến

Dạng 1: Tìm những tỉ trọng trong những cạnh và tính phỏng lâu năm của đoạn thẳng

Phương pháp giải:

Với dạng toán này, tao cần thiết lưu ý cho tới vị trị trọng tâm của tam giác.

Với G là trọng tâm của tam giác ABC với AD, BE và CF là tía lối trung tuyến, thời điểm hiện nay tao có:

Dạng 2: Đường trung tuyến với những tam giác đặc biệt 

Đây là dạng toán lối trung tuyến ở những tam giác quan trọng đặc biệt như tam giác cân nặng, tam giác đều hoặc tam giác vuông.

Phương pháp giải:

Ta cần thiết chú ý nhập tam giác cân nặng hoặc tam giác đều thì lối trung tuyến ứng với cạnh lòng phân chia tam giác trở nên nhì tam giác đều nhau.

Như vậy, trải qua nội dung bài viết bên trên mong muốn Dinhnghia.vn đã hỗ trợ chúng ta, quan trọng đặc biệt những em học viên lớp 7 sở hữu một chiếc nom ở tổng quan tiền nhất về khái niệm, những đặc thù của lối trung tuyến nhập tam giác. Các các bạn hãy xem thêm thiệt kỹ và rèn luyện bọn chúng trải qua những bài bác tập luyện ở cuối nội dung bài viết nhằm bắt chắc chắn thêm kiến thức và kỹ năng về khái niệm lối trung tuyến nhé. Chúc các bạn luôn luôn học tập tốt!.

Xem thêm: Phân tích nhiều thức trở nên nhân tử: Lý thuyết, Bài tập luyện nâng lên và Ứng dụng

Xem thêm: Soạn bài Những ngôi sao xa xôi | Ngắn nhất Soạn văn 9.

Tham khảo lối trung tuyến nhập tam giác qua quýt bài bác giảng của cô ý Quỳnh Dư: