Phương trình vô nghiệm Lúc nào? Một trong mỗi việc chúng ta học viên vẫn thông thường gặp gỡ là “tìm m nhằm phương trình vô nghiệm”. Bài viết lách này của GiaiNgo tiếp tục tổ hợp kỹ năng và kiến thức về phương trình vô nghiệm, thể hiện những dạng toán thông thường gặp gỡ về phương trình vô nghiệm và cơ hội giải cụ thể nhất. Hy vọng chung chúng ta học viên tập luyện thêm thắt kỹ năng và kiến thức nhằm sẵn sàng cho những kì thi đua thiệt đảm bảo chất lượng. Cùng tìm hiểu ngay lập tức thôi nào!
Phương trình vô nghiệm là gì?
Phương trình vô nghiệm là phương trình không tồn tại nghiệm nào là. Phương trình vô nghiệm sở hữu tập luyện nghiệm là S = Ø
Bạn đang xem: Phương trình vô nghiệm khi nào? Bài tập tìm m điển hình
Một phương trình rất có thể sở hữu một nghiệm, nhị nghiệm, phụ thân nghiệm,… tuy nhiên cũng rất có thể không tồn tại nghiệm nào là hoặc vô số nghiệm.
Phương trình vô nghiệm Lúc nào? Điều khiếu nại nhằm phương trình vô nghiệm
Phương trình vô nghiệm Lúc nào?
Bất phương trình vô nghiệm <=> a=0 và b xét với lốt > thì b ≤0≤0; với lốt < thì b ≥0.
Điều khiếu nại nhằm phương trình vô nghiệm là gì?
Phương trình số 1 một ẩn:
Phương trình số 1 một ẩn ax + b = 0 vô nghiệm Lúc a = 0, b ≠ 0
Phương trình bậc nhị một ẩn:
Phương trình bậc nhị một ẩn ax + bx + c = 0 vô nghiệm Lúc a ≠ 0, ∆ < 0
Công thức phương trình vô nghiệm
Phương trình số 1 một ẩn:
Xét phương trình số 1 sở hữu dạng ax + b = 0.
Nếu a = 0, b ≠ 0 thì phương trình vô nghiệm.
Phương trình bậc nhị một ẩn:
Xét phương trình bậc nhị sở hữu dạng ax^2 + bx + c = 0 (a ≠ 0).
- Công thức nghiệm tính delta (ký hiệu là ∆).
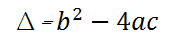
Nếu ∆ < 0 thì phương trình vô nghiệm.
- Công thức sát hoạch gọn gàng tính ∆’ (chỉ tính ∆’ Lúc thông số b chẵn).
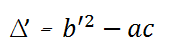
Với b = 2b’
Nếu ∆’ < 0 thì phương trình vô nghiệm.
Một số bài xích khuôn mẫu thăm dò m nhằm phương trình vô nghiệm
Dưới đó là những việc tìm hiểu thêm về dạng toán “tìm m nhằm phương trình vô nghiệm”
Bài 1: Tìm m nhằm phương trình sau vô nghiệm:
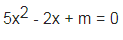
Hướng dẫn:
Do thông số ở biến đổi x2 là một trong những không giống 0 nên phương trình là phương trình bậc nhị một ẩn.
Ta tiếp tục vận dụng ĐK nhằm phương trình bậc nhị một ẩn vô nghiệm vô giải việc.
Để phương trình 5x^2 – 2x + m = 0 vô nghiệm thì ∆’ < 0
⇔ 4 – 5m < 0
⇔ m > ⅘
Vậy với m > ⅘ thì phương trình 5x^2 – 2x + m = 0 vô nghiệm

Bài 2: Tìm m nhằm phương trình sau vô nghiệm:
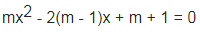
Hướng dẫn:
Do thông số ở biến đổi x2 sở hữu chứa chấp thông số m, nên những khi giải việc tao nên phân tách nhị tình huống là m = 0 và m ≠0.
Xem thêm: Lãnh thổ Trung Quốc rộng lớn tiếp giáp với
Lời giải: Bài toán được tạo thành 2 ngôi trường hợp:
TH1: m = 0
Phương trình phát triển thành phương trình số 1 một ẩn 2x + 1 = 0 ⇔ x = -½ (loại)
Với m = 0 thì phương trình mx^2 – 2(m – 1)x + m + 1 = 0 sở hữu nghiệm x = -½
TH2: m ≠ 0
Phương trình phát triển thành phương trình bậc nhị một ẩn: mx^2 – 2(m – 1)x + m + 1 = 0
Để phương trình vô nghiệm thì ∆’ < 0
⇔ (m – 1)^2 – m.(m + 1) < 0
⇔ m^2 – 2m + 1 – m^2 – m < 0
⇔ -3m < -1
⇔ m > ⅓
Vậy với m > ⅓ thì phương trình mx^2 – 2(m – 1)x + m + 1 = 0 vô nghiệm

Bài 3: Tìm m nhằm phương trình sau vô nghiệm:
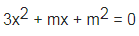
Hướng dẫn:
Do thông số ở biến đổi x2 là một trong những không giống 0 nên phương trình là phương trình bậc nhị một ẩn. Ta tiếp tục vận dụng ĐK nhằm phương trình bậc nhị một ẩn vô nghiệm vô giải việc.
Lời giải: Để phương trình 3×2 + mx + mét vuông = 0 vô nghiệm thì ∆ < 0
⇔ m^2 – 4.3.m^3 < 0
⇔ -11m^2 < 0∀m ≠ 0
Vậy với từng m ≠ 0 thì phương trình 3×2 + mx + mét vuông = 0 vô nghiệm.
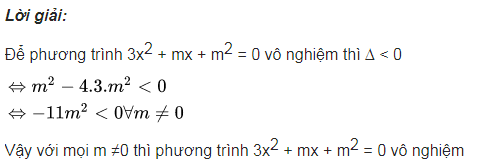
Bài 4: Tìm m nhằm phương trình sau vô nghiệm
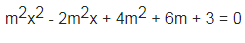
Hướng dẫn:
Do thông số ở biến đổi x2 sở hữu chứa chấp thông số m, nên những khi giải việc tao nên phân tách nhị tình huống là m = 0 và m ≠0.
Lời giải:
- TH1: m = 0
Phương trình phát triển thành phương trình số 1 một ẩn 0x = -3 (phương trình vô nghiệm)
Với m = 0 thì phương trình vô nghiệm
- TH2: m ≠ 0
Để phương trình m2x2 – 2m2x + 4m2 + 6m + 3 = 0 vô nghiệm thì ∆’ < 0
⇔ (-m^2)^2 – m^2 (4m^2 + 6m + 3) < 0
⇔ -3m^4 – 6m^3 – 3m^2 < 0
⇔ -3m^2 .(m^2 + 2m +1) < 0
⇔ -3m^2 .(m+1)^2 < 0∀m ≠ m-1
Xem thêm: Công thức tính số liên kết pi
Vậy với từng m ≠ – 1 thì phương trình m2x2 – 2m2x + 4m2 + 6m + 3 = 0 vô nghiệm

Như vậy nội dung bài viết bên trên vẫn trả lời được vướng mắc Phương trình vô nghiệm Lúc nào? Đồng thời với những bài xích tập luyện khuôn mẫu nhưng mà GiaiNgo share, kỳ vọng sẽ hỗ trợ chúng ta nắm rõ kỹ năng và kiến thức và tập luyện đảm bảo chất lượng rộng lớn. Chúc chúng ta học hành tốt!