Cho hình thang ABCD (AB // CD). Kẻ đường thẳng vuông góc với AC tại C và đường thẳng vuông (Miễn phí)

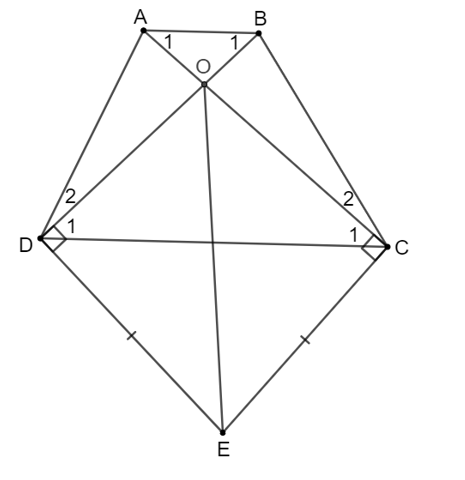
Gọi O là phú điểm của AC và BD.

Bạn đang xem: Cho hình thang ABCD (AB // CD). Kẻ đường thẳng vuông góc với AC tại C và đường thẳng vuông (Miễn phí)

Xét ∆DOE và ∆COE có:

$\widehat{ODE}=\widehat{OCE}=90°$ (vì OD ⊥ DE; OC ⊥ CE)

EC = ED (giả thiết)

Cạnh OE chung

Do cơ ∆DOE = ∆COE (cạnh huyền – cạnh góc vuông).

Suy đi ra OC = OD (hai cạnh tương ứng).

Do cơ tam giác OCD cân nặng bên trên O nên ${\widehat{C}}_1={\widehat{D}}_1$.

Vì ABCD là hình thang nên AB // CD suy đi ra ${\widehat{A}}_1={\widehat{C}}_1;{\widehat{B}}_1={\widehat{D}}_1$ (cặp góc ví le trong).

Do cơ ${\widehat{A}}_1={\widehat{B}}_1$ (vì ${\widehat{C}}_1={\widehat{D}}_1$).

Suy đi ra tam giác OAB cân nặng bên trên O nên OA = OB.

Xem thêm: Nguyên hàm cosx - Tính nguyên hàm

Xét ∆OAD và ∆OBC có:

OA = OB (chứng minh trên)

$\widehat{AOD}=\widehat{BOC}$ (hai góc đối đỉnh)

OC = OD (chứng minh trên)

Do cơ ∆OAD = ∆OBC (c.g.c)

Suy đi ra ${\widehat{C}}_2={\widehat{D}}_2$ (hai góc tương ứng).

Ta với $\widehat{ADC}={\widehat{D}}_1+{\widehat{D}}_2;\widehat{BCD}={\widehat{C}}_1+{\widehat{C}}_2$.

Mà ${\widehat{C}}_1={\widehat{D}}_1 ;{\widehat{C}}_2={\widehat{D}}_2$ nên $\widehat{ADC}=\widehat{BCD}$.

Xem thêm: Công thức tính số liên kết pi

Hình thang ABCD với $\widehat{ADC}=\widehat{BCD}$ nên ABCD là hình thang cân nặng.

Câu 2: